The requirement for a (very) large training set is generally the main critic that is formulated against deeplearning algorithms.  In this blog, we show how deep convolutional neural networks (CNN) can be used in an unsupervised manner to identify similar images in a set.  At first, we remind the general concepts behind convolutional neural networks.  In a second step, we discuss the VGG16 algorithm and how it was trained.  We then explain the concepts of transfer learning and retraining.  After that, we have all the ingredients to introduce the reverse image search algorithm.  Finally, we will show a demo of the reverse image search performance with a deck of cards.
 

Convolutional neural network

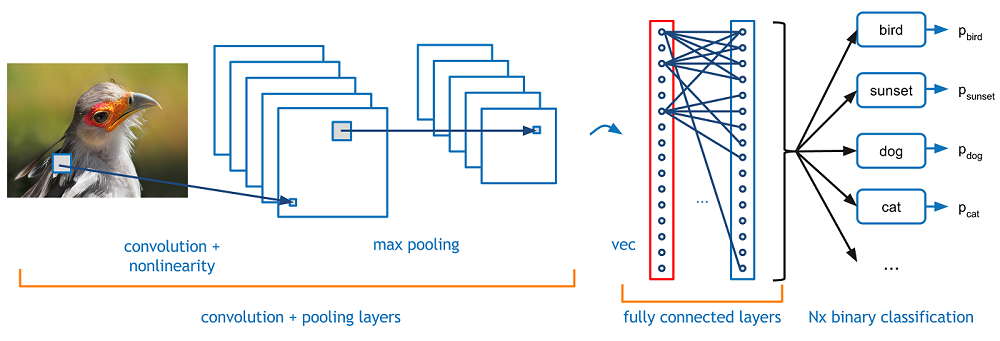
Convolutional neural network (CNN or ConvNet) is a type of artificial neural network that was initially developed by Yann LeCun (and friends) for image recognition.  As for the regular neural network, they are made up of neurons that have learnable weights and biases. Each neuron receives some inputs, performs a linear operation (input * weights + bias) and optionally follows it with a non-linear activation function (generally a Sigmoid or a Relu). The major difference with respect to a regular neural network is that ConvNets are translation invariant.  This an important property for object recognition in images because we want the neural network to identify the object regardless on its position on the image.  Intuitively, one way to achieve this requirement would be to divide the picture into many smaller-size pads and apply a unique (reduced) neural network on each of these pads.  Therefore, if the object that we are trying to identify is present on the bottom-left corner of the image instead of the top-right corner, we would still be capable of finding it as soon as we have a picture pad covering that region.  We can actually go further and split the pads into smaller pads made up of the constituent of the objects we are trying to identify.  Etc. Etc.  This is the general idea behind convolutional neural networks.

ConvNets are generally made of two alternating types of layers:

• Convolutional Layers
  This is the layer that does most of the computational work.  It is made of a certain number of learnable kernels/filters that are have reduced width/height extension compared to the size of the image but are sensitive to the full image depth (used to encode the color of the image pixels).  During the forward pass of the network, the filters are locally convoluted with all possible image pads of the filter dimension.  The local (convolution) output of the layer is then passed through an activation function (generally a Relu).  When the learnable pattern of the filter matches the local pattern of the image, the output of this process is generally close to 1 otherwise it is close to 0.  The convolutional layer output is, therefore, a local indicator of pattern identification on the picture. 
  The filter patterns are learned using regular neural network backpropagation and gradient descent technique.

• Pooling Layers
  The main goal of the pooling layer is to reduce the spatial size of the image representation (after a convolutional layer) in order to reduce the number of learnable parameters in subsequent layers.  This layer is basically a non-linear downsampling of the image representation.  Very often, the spatial dimension is reduced by a factor n=2 or 3 by keeping only the value of the largest pixel in a group of n x n pixels. 

A ConvNet is generally made up of several pairs of convolutional + pooling layers and ended with one or two fully connected layers as we can find them in a multi-layer perceptron.  The first convolutional layers generally learn to identify simple (very local) patterns like vertical lines, horizontal lines, diagonals, etc.  While the following layers are made up of patterns of these simple patterns are good at identifying more complex patterns.  For instance, could learn that a car is made up of "wheel" and "windshield" patterns.   The purpose of the final layers is to make a prediction based on the presence of pattern at specific locations in the image representation.  The figure bellow, taken from this excellent blog, shows the typical architecture of a ConvNet.

We stop here the ConvNet introduction as we don't need a deep theory understanding for the following of this blog.  If you'd like to know more about CNN, the web is full of pedagogical introductive courses to ConvNets (see for instance this, this or this). 

ImageNet and the VGG16 network

The total number of free parameters in a convNet is significantly smaller than for a multi-layer perceptron achieving the same job.  Nonetheless, the number of parameters to learn in a modern convNet is generally still pretty large (order of billions) and require a large training set to avoid overfitting.

The purpose of the ImageNet database is to provide such training datasets in order to accelerate the research in image recognition.  Thanks to imageNet, we have access to 15M pictures that are labeled by one or more category.  They are currently about 20K different category label (or synsets).  In addition, the ImageNet group organizes yearly image recognition challenges where the word class researchers can compare the performances of their algorithms.  For this blog, we are in particular interested in the Task 2a of the 2014 contest, The goal was to classify 50K pictures among a 1000 different label categories.  Identified object are also asked to be localized on the picture.  A training set of 1.2M images was provided.

One of the main winners of this competition is the VGG16 algorithm that was developed by the famous Visual Geometry Group (VGG) of the University of Oxford.  The algorithm is documented in great details in this scientific article.  They are also many pedagogical introductions to the algorithm all over the web, so I am just going to give a brief summary here.  The VGG16 algorithm is made up of 5 convolutional blocks followed by 3 fully-connected dense layers.  The inputs are images of size 224 pixels (width) x 224 pixels (height) x 3 color components (depth) and the output is a vector of 1000 components giving the probability that the input image belong to each of the possible label categories.  The network is made of 16 "active" layers that are listed hereafter.  The number in parenthesis provides the tensor dimensions of each layer outputs:

• Input Layer (224x224x3)

• CNN Block 1

  • Convolutional Layer1 (224x224x64)

  • Convolutional Layer2 (224x224x64)

  • Pooling Layer (112x112x64)

• CNN Block 2

  • Convolutional Layer1 (112x112x128)

  • Convolutional Layer2 (112x112x128)

  • Pooling Layer (56x56x128)

• CNN Block 3

  • Convolutional Layer1 (56x56x256)

  • Convolutional Layer2 (56x56x256)

  • Convolutional Layer3 (56x56x256)

  • Pooling Layer (28x28x256)

• CNN Block 4

  • Convolutional Layer1 (28x28x512)

  • Convolutional Layer2 (28x28x512)

  • Convolutional Layer3 (28x28x512)

  • Pooling Layer (14x14x512)

• CNN Block 5

  • Convolutional Layer1 (14x14x512)

  • Convolutional Layer2 (14x14x512)

  • Convolutional Layer3 (14x14x512)

  • Pooling Layer (7x7x512)

• Flatten Layer (25088 = 7x7x512)

• Dense Layer (4096)

• Dense Layer (4096)

• Dense (Softmax) Layer (1000)

The accuracy of the algorithm at identifying 1000 different objects on images is about 93%.  This is a very high accuracy when we know that the accuracy of humans for the same task is about 95% as explain in this paper.  Today, they are more sophisticated algorithms that can even outperform human performances for such tasks.

Now that we know the VGG16 network configuration and that we have a large publicly available training set, we are ready to train the algorithm...  We only need to use the 1.5million training set to learn 139 million learnable parameters through backpropagation...  Hum... that's going to really take a while on a personal computer.  Computing resources are actually the bottleneck here....

Fortunately, pre-trained weights for the VGG16 algorithm (and many others) are publicly available on the Caffe Model Zoo web page.  The python deeplearning library Keras even have automatic scripts to download the weights when needed.  So we have in our hands one of the most accurate algorithms for image recognition that is already pre-trained and ready to use.
 

Transfer Learning 

What is interesting with convolutional neural networks, is that each of the convolutional layers is learning specific image features (lines, colors, patterns, groups of pixels, etc.).  It's only at the very end of the network that all these image features are connected to each other in view of tagging the entire image.  So, although the end of the network is highly specialized at recognizing the thousand possible labels of the 2014 ImageNet contest, the lower parts of the network are more generic and could be recycled for other tasks without retraining.  This is often referred to as "transfer learning".

Thanks to transfer learning, we could replace the last layer(s) of the network by something that is more dedicated to our use case (different than the 1000 ImageNet labels).  For instance, if we are interested in finding whether our image contains either a Cat or a Dog, we would have only two different labels and our last layer could be made of only two neurons (compared to the 1000 of the VGG16).  If we assume that the rest of the network should remain unmodified, we would have to learn only 8194 free parameters (corresponding to 2 bias value and all weight connections between the 4096 neurons of the one to the last layer with the 2 neurons of the last layer).  This is a very small number of parameters to learn for such a complex task.  We would, therefore, need a relatively small training dataset to train our specialized VGG16 algorithm.

Depending on the problem, the hypothesis the first VGG16 layers remains totally unchanged might not be always good.  In these cases, we may want to entirely re-train the algorithm and therefore find the optimal values for all of the 139M parameters of the network.  But even in that situation, the transfer learning is a useful thing as we could start with parameter values that are already close to their minimum.  This would make the algorithm to converge much much faster.  Training time could easily be reduced from weeks to hours timescale.
 

Unsupervised usage of the VGG16 algorithm for Reverse Image Search

So far, we have explained how we can train the VGG16 using super large training dataset, and how to "recycle" pre-trained model in order to accommodate a smaller training set to perform simpler tasks.  But, we can go further and recycle the VGG16 pre-trained model to perform a very useful task that would not even need a small retraining.  This would, therefore, move this to the category of "unsupervised" model that is immediately ready to use. 

If we drop the very last layer of the VGG16 (as shown in the figure bellow), the output of the network is a vector of 4096 components.  Those components are the one that is used by VGG16 to make the difference between cats, dogs, cars and many other types of images.  Thus, they contain lots of information about the content of the image in a relatively compact way.  We like to see the output of the vector as the DNA of the picture that is analyzed by the last layer to name the content of the image.  So, somehow after this layer, the object is already "uniquely" identified... it's just that we don't know how to call it.

In the following, we would refer to this modified VGG16 algorithm as the "topless" VGG16.

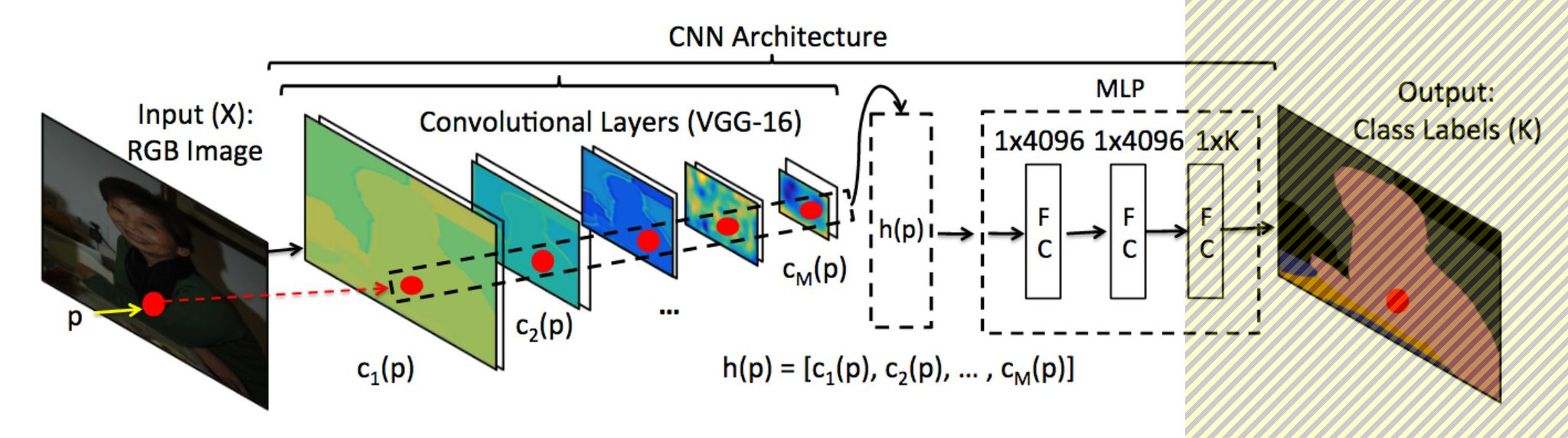
They are many tasks that actually do not require to name the content of the image.  Think for instance to a task where you have an image and you'd like to identify all other images that look like this one.  The topless VGG16 algorithm would be very good at this, as similar images would have similar DNA content.  So the complex problem of finding similar images in a collection is transformed to the trivial problem of finding similar vectors.  This is achieved very easily by linear algebra and more precisely by the dot product of the two vectors.  If you are not familiar with this concept, you can search for cosine similarity on the web.

Most of the Reverse Image Search services, like TinEye or Google image search, rely on such technique for comparing images.

In the following of this blog, we will show how the technique perform in a simple example.
 

Demonstration of the reverse image search on a deck of card

We will show the performance of the topless VGG16 algorithms for identifying similar cards out of two shuffled decks of cards.  In order to make the exercise a bit more tricky, we used two decks of cards with very different image styles and very different image resolutions and dimensions.  The first one as 166x116 dimensions, while the second one has 91x67 dimensions.  Both will be resized to 224x224 dimensions has this is the expected input size of the VGG16 algorithm.  The figure bellow shows the 104 cards that we are going to use.

Every card is passed through the topless VGG16 in order to get its associated DNA vector.  The vectors are then normalized to norm=1 and used to compute the similarity between the ith card and the jth card by computing the cosine similarity (dot product) of the two vectors.  Finally, we can build the similarity matrix which would contain the similarity between all pair of cards.  The matrix is analyzed to find out what are the 5 most similar cards to a given one.

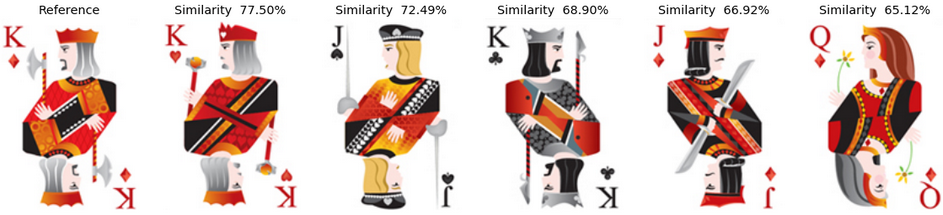
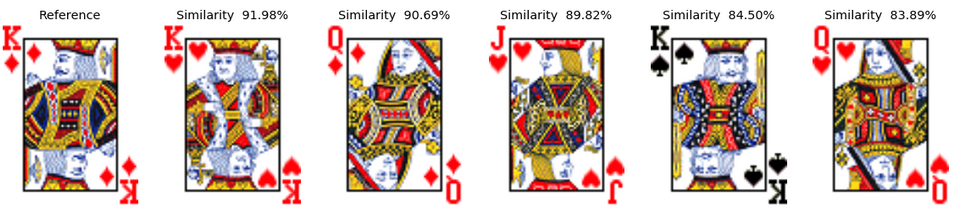
Let's look at the most similar cards (as predicted by the topless VGG16 also) for a few examples.  In the pictures here after, the left most card is always the reference card for which we are trying to identify the top-5 most similar cards.  The value of the cosine similarity between the two picture DNA vectors is also given at the top of most similar images.

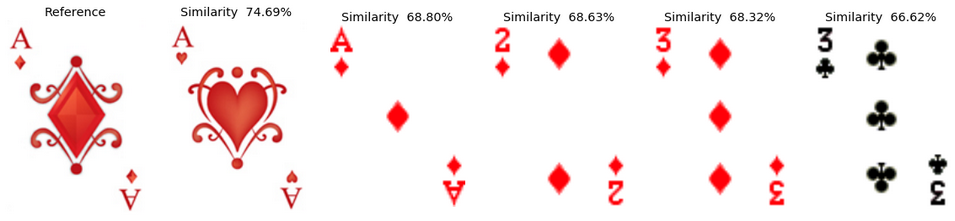
Example 1: The Ace of Diamonds
In both decks of cards, the most similar card to the ace of diamonds is identified as the ace of hearts of the same deck.  Interestingly, for the second most similar card, we have different results depending on the deck.  For deck1, the ace of diamonds of the other deck is tagged as the second to most similar.  For deck2, on the contrary, it spots the 2 of diamonds as being more similar than the ace of the other deck.  In both decks, the 2 and 3 of diamonds are marked as rather similar to the ace, which makes sense as in all cases, there are diamond symbols in the top left and bottom right of the card, and the overall card symmetry is similar. 

 

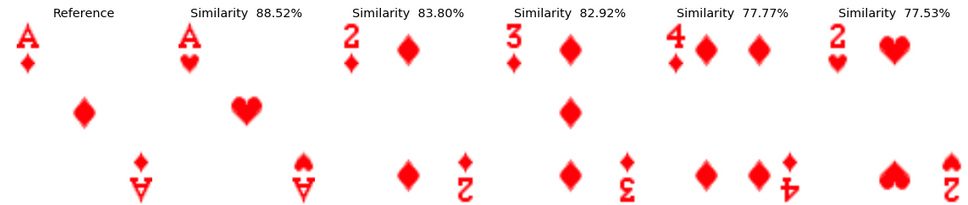
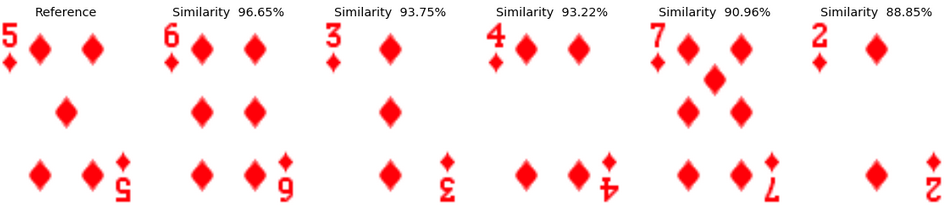
Example 2: The Five of Diamonds
In both decks of cards, the most similar card to the five of diamonds is identified as the six of diamonds in the same deck.  Interestingly, the following cards are similar in both decks and have all a rather close similarity value, which explain why the order is not necessarily identical.  All these cards actually have a value that is close to 5:  3,4,6,7.  This makes perfect sense.

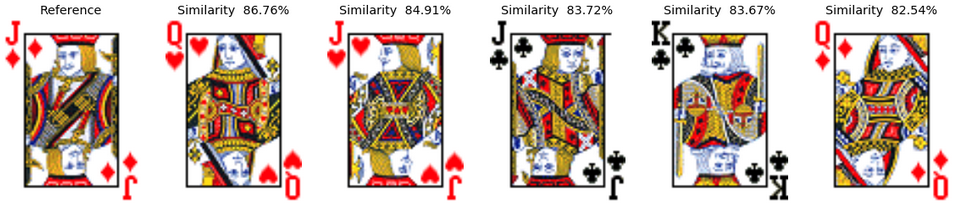
Example 3: The Jack of Diamonds
Here, the image on the cards become much more complex and the behavior of the algorithm is, therefore, a bit less clear.  What we noticed, is that the direction of the character face, the color of the character hair, the style of the weapons and the clothes colors are all playing an important role in the card similarity.  These features matter much more than the card color.  Wich also makes perfect sense as these features occupy quite a large part of the picture  (much more than the card color symbols).  We can also notice that the similarity between cards is also lower than in the previous case.

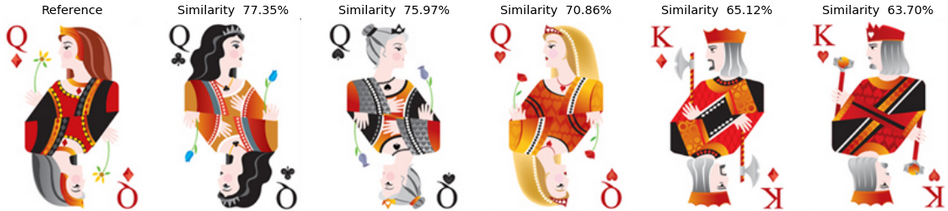
Example 4: The Queen of Diamonds
Similarly, to what was discussed in example 3, as the images are quite rich in terms of features, it is more difficult to understand the deep reasons behind the similarity scores.  But clearly, the clothes styles seems to have quite some importance here.

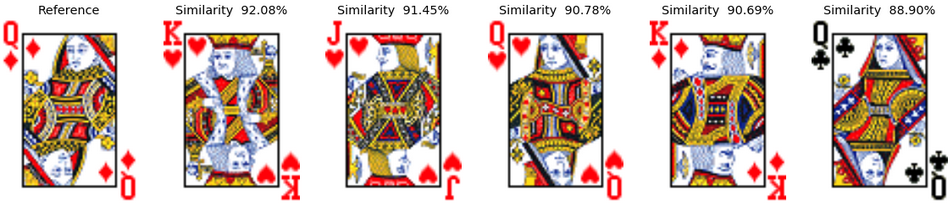
Example 5: The King of Diamonds
Finally, we can have a look at the results for the king of diamonds.  Interestingly, in the deck1, it identifies left looking "male" cards, then the right looking "male" and finally the queen of diamonds.  In the second deck, the resolution of the picture is much worse, but we despite that we can see a similar kind of behavior. 

Conclusion

In conclusion, we have seen that convolutional neural networks are quite large neural networks with hundreds of millions of learnable parameters that are generally hard to train by individuals with limited computing resources.  However, we have also explained that transfer learning allows individuals to recycle pre-trained models for other purposes with minimal (re)training or even without retraining at all for the case of reverse image search.  We have demonstrated that the convolutional neural networks are capable of extracting the features associated with an image into the form of a picture DNA vector.  Comparing these DNA vectors allows identifying pictures that have the similar type of features and that are therefore similar to each other.

 

Have you already faced similar type of issues ?  Feel free to contact us, we'd love talking to you…

If you enjoyed reading this post, please like it. It doesn't cost you anything, but matters for me!